MD5

MD5消息摘要算法（英语：MD5 Message-Digest Algorithm），一种被广泛使用的密码散列函数，可以产生出一个128位（16个字符(BYTES)）的散列值（hash value），用于确保信息传输完整一致。将数据（如一段文字）运算变为另一固定长度值，是散列算法的基础原理。

参考

MD5破解的几种方法

Wiki MD5

特性

不可逆向的
我们没办法把MD5码还原对应的原文。道理很简单，任意长度的数据经过MD5处理后，所包含的信息量已经大大减少，那是不可能再次还原成为原始信息的。

原文中作一个小变化其散列也会发生巨大的变化

1 2	`MD5("The quick brown fox jumps over the lazy dog") = 9e107d9d372bb6826bd81d3542a419d6`

比如用c取代d, 其MD5值发生了巨大的变化

1 2	`MD5("The quick brown fox jumps over the lazy cog") = 1055d3e698d289f2af8663725127bd4b`

已被破解
通俗点讲就是，可以找到一个A和一个B，使hash（A）=hash（B），而真正有用的是给定一个A能得到B，使hash（A）=hash（B），而王小云能做到这样

应用

MD5 摘要已在软件世界中广泛使用，以确保传输的文件已完好无损地到达。例如，文件服务器通常会为文件提供预先计算的 MD5（称为md5sum）校验和，以便用户可以将下载文件的校验和与其进行比较。

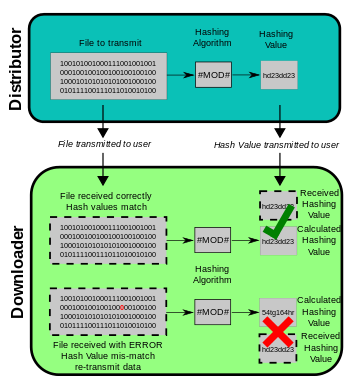
由于很容易产生 MD5 冲突，因此创建文件的人可能会创建具有相同校验和的第二个文件，因此该技术无法防止某些形式的恶意篡改。

在某些情况下，校验和是不可信的（例如，如果它是通过与下载文件相同的渠道获得的，他人可能修改了文件后再次修改了MD5，使得MD5并不可信），在这种情况下，MD5 只能提供错误检查功能：“它会识别损坏或不完整的下载，这变成下载较大文件时更有可能。”

破解

穷举法&字典法

穷举法非常简单，就是不停地尝试各种字符的排列组合，看哪一个组合的MD5码能对上。可惜缺点是太耗费时间了。我们举个栗子，假设我们要破解一个6位大小写字母和数字混合的密码，那么一共有(26+26+10)⁶ 种组合。这个数的大小超过500亿。

既然计算如此费时，能不能考虑把计算结果以映射表的形式存放起来，一个萝卜一个坑，一个原文对应着一个MD5码呢？可以呀！这就是传说中的“字典法”。将已知的MD5码查表，直接反查出原文。字典法体现了算法设计的“以空间换时间”的思想。缺点是比较耗费空间。不过现在硬盘的价格变得白菜价了，空间开销不算什么。

CMD5 反查网站

SMD5 反查网站

哈希链表&彩虹表法

如果说穷举法太耗费时间，字典法太耗费存储空间的话，我们能不能考虑在时间消耗和空间消耗之间折中呢？我们可以考虑用链表将一系列有意义的原文和MD5码串起来。
要构造这样的链表，我们需要两个函数：哈希函数H(x)和衰减函数（reduction function）R(x)。哈希函数可以是MD5，也可以是其他的消息摘要算法。H(x)的值域是R(x)的定义域，R(x)的值域是H(x)的定义域。R(x)不是H(x)的反函数。
将一个原文不停地使用H(x)和R(x)交替进行运算k次，再将原文本身和运算结果以链表的形式串接起来，就可以得到结点个数为2k+1的链表。实际存放的时候只存放首端和末端两个原文即可。这种链表叫做“哈希链表”，体现了算法设计的“时空权衡”（Space and Time Tradeoffs）。
举个栗子，假设原文s=abcabc，经过2次交替运算，得到以下的链表：
abcabc->H(x)->3C8B0D7A->R(x)->eopmca->H(x)->7E9F216C->R(x)->rapper
以上数据均为举例编造的，仅为说明原理使用。那我们存放这个链表的时候，只需要记录abcabc和rapper两个原文即可。
假设我们要破解的摘要值（哈希链表的H(x)不一定是MD5算法，这里用更准确的说法代替MD5码）是7E9F216C，经过R(x)运算得到rapper，说明我们要寻找的原文就在以rapper为末端的哈希链表中。从首端开始经过多次运算，我们发现eopmca的摘要值就是7E9F216C。于是就反查出7E9F216C对应的原文是eopmca。
如果在生成哈希链表的时候依次使用多个不一样的R(x)，此时的哈希链表就是“彩虹表”。
这里有已经计算好的彩虹表：http://project-rainbowcrack.com